$$ \def\ind{{\perp\!\!\!\perp}} \def\nind{{\not\!\perp\!\!\!\perp}} $$

为了介绍工具变量，我们首先要从线性模型出发。毫无疑问，线性模型是理论和应用统计（包括计量经济学和流行病学等）最重要的工具；对线性模型的深刻理解，可以说就是对一大半统计理论的理解。下面的第一部分先对线性模型，尤其是线性模型背后的假设做一个回顾。

一、线性回归和最小二乘法

线性模型和最小二乘的理论起源于高斯的天文学研究，“回归”（regression）这个名字则是 Francis Galton 在研究优生学的时候提出来的。为了描述的方便，我们假定回归的自变量只有一维，比如个体$i$是否接受某种处理（吸烟与否；参加某个工作；等等），记为$D_i$。 回归的因变量也是一维，表示我们关心的结果（是否有肺癌；是否找到工作培训与否；等等），记为$Y_i$。假定我们的研究中有 $n$ 个个体，下面的线性模型用于描述$D$和$Y$之间的“关系”：

$$Y_i = \alpha + \beta D_i + \varepsilon_i, i=1, \cdots, n. \quad \quad (1)$$

一般情形下，我们假定个体间是独立的。模型虽简单，我们还是有必要做一些解释。首先，我们这里的讨论都假定$D_i$是随机变量，对应统计学中的随机设计 （random design）的情形；这和传统统计学中偏好的固定设计（fixed design）有点不同—那里假定$D_i$总是固定的。（统计学源于实验设计，那里的解释变量都是可以控制的，因此统计学教科书有假定固定设计的传统。）假定$D_i$是随机的，既符合很多社会科学和流行病学的背景，又会简化后面的讨论。另外一个问题是 $\varepsilon_i$，它到底是什么含义？Rubin 曾经嘲笑计量经济学家的$\varepsilon_i$道：为了使得线性模型的等式成立，计量经济学家必须加的一项，就叫$\varepsilon_i$。批评的存在并不影响这个线性模型的应用；关键的问题在于，我们在这个$\varepsilon_i$上加了什么假定呢？最根本的假定是：

$$ E(\varepsilon_i) = 0, \text{ and }  \text{cov}(D_i, \varepsilon_i) = 0. \quad \quad (2) $$

不同的教科书稍有不同，比如 Wooldridge 的书上假定$E(\varepsilon_i\mid D_i ) =0$，很显然，这蕴含着上面两个假定。零均值的假定并不强，因为 $\alpha$ “吸收”了$\varepsilon_i$的均值；关键在第二个协方差为零的假定—它通常被称为“外生性”（exogeneity）假定。在这个假定下，我们在 (1) 的两边关于$D_i$取协方差，便可以得到：

$$\text{cov}(Y_i, D_i )= \beta \text{var}(D_i),$$

因此，$\beta = \text{cov}(Y_i, D_i) / \text{var}(D_i)$，我们立刻得到了矩估计：

$$\widehat{\beta}_{OLS} =  \frac{ \sum_{i=1}^n (Y_i – \bar{Y}) (D_i – \bar{D}) } {  \sum_{i=1}^n (D_i – \bar{D})^2  }.$$

上面的估计式也是通常的最小二乘解，这里只是换了一个推导方式。如果将 (1) 看成一个数据生成的机制，在假定 (2) 下我们的确可以估计出因果作用$\beta$.

二、内生性和工具变量

问题的关键是假定 (2) 很多时候并不成立（$\text{cov}(D_i, \varepsilon_i)\neq 0$），比如，吸烟的人群和不吸烟的人群本身很不相同，参加工作培训的人可能比不参加工作培训的人有更强的找工作动机，等等。因此，包含个体$i$其他所有隐藏信息的变量$\varepsilon_i$不再与$D_i$不相关了—这被称为“内生性”（endogeneity）。这个时候，最小二乘估计收敛到$\beta + \text{cov}(D,\varepsilon)/\text{var}(D)$, 因而在$\text{cov}(D,\varepsilon)\neq 0$时不再是$\beta$的相合估计。

前面几次因果推断的介绍中提到，完全的随机化实验，可以给我们有效的因果推断。但是很多问题中，强制性的随机化实验是不现实或者不符合伦理的。比如，我们不能强制某些人吸烟，或者不吸烟。但是，“鼓励性实验”依然可行。我们可以随机地给吸烟的人以某种金钱的奖励，如果他们放弃吸烟，则获得某种经济上的优惠。将这个“鼓励性”的变量记为$Z_i$，它定义为是否被鼓励的示性变量，取值 0-1。由于我们的鼓励是完全随机的，有理由假定$\text{cov}(Z_i, \varepsilon_i)=0$。

以上的各个假定，可以用下面的一个图来形象的描述。

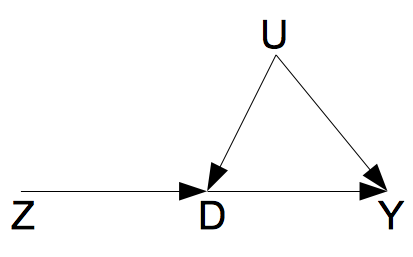
如图所示，由于$D$和$Y$之间存在一个混杂因素$U$，两者之间的因果作用是不可以用线性回归相合估计的。工具变量$Z$的存在，使得$D$到$Y$的因果作用的识别成为了可能。这里的工具变量$Z$满足如下的条件: $Z\ind U, Z\nind D$，并且$Z\ind Y|(D,U)$。第三个条件，可以理解成为“无 $Z$到$Y$的直接作用”。

此时，我们在线性模型 (1) 两边关于$Z_i$取协方差，得到

$$\text{cov}(Z_i, Y_i) = \beta \text{cov} (Z_i, D_i),$$

因此，$\beta = \frac{  \text{cov}(Z_i, Y_i)} {\text{cov} (Z_i, D_i) } $，我们立刻得到如下的矩估计：

$$\widehat{\beta}_{IV} = \frac{ \sum_{i=1}^n (Y_i – \bar{Y}) (Z_i – \bar{Z})}{ \sum_{i=1}^n (D_i – \bar{D}) (Z_i – \bar{Z}) } .\quad \quad (3)$$

根据大数定律，这个“工具变量估计”是$\beta$的相合估计量。上面的式子对一般的$Z_i$都是成立的；当$Z_i$是 0-1 变量时，上面的式子可化简成：

$$\widehat{\beta}_{IV} = \frac{  \bar{Y}_1 – \bar{Y}_0 } { \bar{D}_1 – \bar{D}_0 },$$

其中$\bar{Y}_1$表示$Z_i=1$组的平均结果，$\bar{Y}_0$表示$Z_i=0$组的平均结果，关于$D$的定义类似。上面的估计量，很多时候被称为 Wald 估计量（它的直观含义是什么呢？） 需要注意的是，(3) 要求$\text{cov}(Z_i,D_i)\neq 0$，即“鼓励”对于改变人的吸烟行为是有效的；否则上面的工具变量估计量在大样本下趋于无穷大。

三、潜在结果视角下的因果作用

工具变量估计量在文献中存在已有很多年了，一直到了 Angrist, Imbens and Rubin (1996) 年的文章出现，才将它和潜在结果视角下的因果推断联系起来。关于 Neyman 引进的潜在结果，需要回顾这一系列的第二篇文章。

一般地， $Z$表示一个 0-1 的变量，表示随机化的变量（1 表示随机化分到非鼓励组；0 表示随机化分到鼓励组）；$D$ 表示最终接受处理与否（1 表示接受处理；0 表示接受对照）；$Y$ 是结果变量。为了定义因果作用，我们引进如下的潜在结果：$(Y_i(1), Y_i(0))$表示个体$i$接受处理和对照下$Y$的潜在结果；$(D_i(1), D_i(0))$表示个体$i$非鼓励组和鼓励组下$D$的潜在结果。由于随机化，下面的假定自然的成立：

（随机化）$Z_i \ind \{ D_i(1), D_i(0), Y_i(1), Y_i(0) \}.$

根据鼓励性实验的机制，个体在受到鼓励的时候，更加不可能吸烟，因为下面的单调性也是很合理的：

（单调性）$D_i(1) \leq D_i(0).$

由于个体的结果$Y$直接受到所受的处理$D$的影响，而不会受到是否受鼓励$Z$的影响，下面的排除约束（exclusion restriction）的假定，很多时候也是合理的：

（排除约束）$D_i(1) = D_i(0)$ 蕴含着 $Y_i(1) = Y_i(0)$.

上面的假定表明，当随机化的“鼓励”$Z$不会影响是否接受处理$D$时，随机化的“鼓励” $Z$也不会影响结果变量$Y$。也可以理解成，随机化的“鼓励” $Z$ 仅仅通过影响是否接受处理$D$来影响结果$Y$，或者说，随机化“鼓励” $Z$本身对与结果变量$Y$没有“直接作用”。

以上三个假定下，我们得到： $$ \begin{eqnarray*} &&ACE(Z \rightarrow Y) \\ & = & E\{Y_i(1)\} -E\{Y_i(0)\} \\ &=& P\{ D_i(1)=1, D_i(0)=0\} E\{Y_i(1)-Y_i(0)\mid D_i(1)=1, D_i(0)=0 \}\\ &&+ P\{ D_i(1)=0, D_i(0)=0\} E\{Y_i(1)-Y_i(0)\mid D_i(1)=0, D_i(0)=0 \}\\ &&+P\{ D_i(1)=1, D_i(0)=1\} E\{Y_i(1)-Y_i(0)\mid D_i(1)=1, D_i(0)=1 \}\\ &=& P\{ D_i(1)=1, D_i(0)=0\} E\{Y_i(1) -Y_i(0)\mid D_i(1)=1, D_i(0)=0 \}. \end{eqnarray*} $$

单调使得 $D$ 的潜在结果的组合只有三种；排除约束假定使得上面分解的后两个式子为$0$。由于对于 $(D_i(1)=0, D_i(0)=0)$ 和 $(D_i(1)=1, D_i(0)=1)$两类人，随机化的“鼓励”对于$D$的作用为$0$，$(D_i(1)=1, D_i(0)=0)$一类人的比例就是$Z$对$D$平均因果作用：$ACE(Z\rightarrow D) = P\{ D_i(1)=1, D_i(0)=0\} $. 因此，

$$ CACE= E\{Y_i(1)-Y_i(0)\mid D_i(1)=1, D_i(0)=0 \} = \frac{ ACE(Z \rightarrow Y) }{ ACE(Z\rightarrow D) }. $$

上面的式子被定义为$CACE$是有理由的。它表示的是子总体$(D_i(1)=1, D_i(0)=0)$中，随机化对于结果的因果作用；由于这类人中随机化和接受的处理是相同的，它也表示处理对结果的因果作用。这类人接受处理与否完全由于是否接受鼓励而定，他们被成为“依从者”（complier），因为这类人群中的平均因果作用又被成为“依从者平均因果作用”（CACE：complier average causal effect）;计量经济学家称它为“局部处理作用”（LATE：local average treatment effect）。

由于$Z$是随机化的，它对于$D$和$Y$的平均因果作用都是显而易见可以得到的。因为$\widehat{ACE}(Z\rightarrow D) = \bar{D}_1 – \bar{D}_0, \widehat{ACE}(Z\rightarrow Y) = \bar{Y}_1 – \bar{Y}_0$，CACE 的一个矩估计便是

$$ \frac{\widehat{ACE}(Z\rightarrow Y)  } {  \widehat{ACE}(Z\rightarrow D)   } = \widehat{\beta}_{IV}.$$

由此可见工具变量估计量的因果含义。上面的讨论既显示了工具变量对于识别因果作用的有效性，也揭示了它的局限性：我们只能识别某个子总体的平均因果作用；而通常情况下，我们并不知道某个个体具体属于哪个子总体。

四、实例

这部分给出具体的例子来说明上述理论的应用，具体计算用到了第五部分的一个函数（其中包括用delta方法算的抽样方差）。这里用到的数据来自一篇政治学的文章 Green et al. (2003) “Getting Out the Vote in Local Elections: Results from Six Door-to-Door Canvassing Experiments”，数据点击此处可以在此下载。

文章目的是研究某个社会实验是否能够提高投票率，实验是随机化的，但是并非所有的实验组的人都依从。因此这里的变量 $Z$ 表示随机化的实验，$D$ 表示依从与否，$Y$ 是投票与否的示性变量。具体的数据描述，可参加前面提到的文章。

原始数据总结如下：

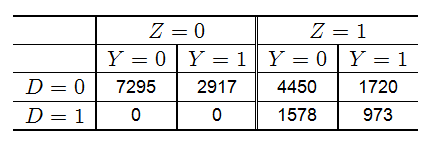
根据下一个部分的函数，我们得到如下的结果：

CACE.IV(Y, D, Z)
$CACE
[1] 0.07914375

$se.CACE
           [,1]
[1,] 0.02273439

$p.value
             [,1]
[1,] 0.0004991073

$prob.complier
[1] 0.2925123

$se.complier
[1] 0.004871619

由此可见，这个实验对于提高投票率，有显著的作用。

五、R code

## function for complier average causal effect
CACE.IV <- function(outcome, treatment, instrument) {
  Y <- outcome
  D <- treatment
  Z <- instrument
  N <- length(Y)

  Y1 <- Y[Z == 1]
  Y0 <- Y[Z == 0]
  D1 <- D[Z == 1]
  D0 <- D[Z == 0]

  mean.Y1 <- mean(Y1)
  mean.Y0 <- mean(Y0)
  mean.D1 <- mean(D1)
  mean.D0 <- mean(D0)

  prob.complier <- mean.D1 - mean.D0
  var.complier <- var(D1) / length(D1) + var(D0) / length(D0)
  se.complier <- var.complier^0.5

  CACE <- (mean.Y1 - mean.Y0) / (mean.D1 - mean.D0)

  ## COV
  pi1 <- mean(Z)
  pi0 <- 1 - pi1

  Omega <- c(
    var(Y1) / pi1, cov(Y1, D1) / pi1, 0, 0,
    cov(Y1, D1) / pi1, var(D1) / pi1, 0, 0,
    0, 0, var(Y0) / pi0, cov(Y0, D0) / pi0,
    0, 0, cov(Y0, D0) / pi0, var(D0) / pi0
  )
  Omega <- matrix(Omega, byrow = TRUE, nrow = 4)

  ## Gradient
  Grad <- c(1, -CACE, -1, CACE) / (mean.D1 - mean.D0)

  COV.CACE <- t(Grad) %*% Omega %*% Grad / N

  se.CACE <- COV.CACE^0.5

  p.value <- 2 * pnorm(abs(CACE / se.CACE), 0, 1, lower.tail = FALSE)

  ## results
  res <- list(
    CACE = CACE,
    se.CACE = se.CACE,
    p.value = p.value,
    prob.complier = prob.complier,
    se.complier = se.complier
  )

  return(res)
}